Accueil > Mesures électriques > Inductance en alternatif sinusoïdal monophasé

Récepteur inductif en alternatif monophasé

L'inductance ou plus couramment désignée comme bobine ou bobinage est un composant électrique présent dans de nombreux appareils en électrotechnique. Le contacteur, le télérupteur, un moteur, un transformateur, tous ces appareils contiennent une ou plusieurs inductances nécessire à leur fonctionnement. Mais à quoi sert l'inductance ? Quels sont ses effets dans un circuit électrique monophasé ?
Découvrez dans ce cours pourquoi l'inductance est utile au fonctionnement de nombreux appareils électriques.

Sommaire :
• 1. Qu'est ce qu'une inductance ou bobine ?
• 2. Mesures expérimentales
• 3. Détermination des caractéristiques de la tension et du courant
• 4. Allures de la tension et du courant et vecteur de Fresnel
• 5. Équation du courant et de la tension
• 6. L'inductance sous tension sinusoïdale monophasée
• 7. Conclusion
• 8. Exercices

1. Qu'est ce qu'une inductance ou bobine ? :

On désigne comme étant une inductance l'ensemble des dipôles tels qu'une self ou une bobine, qui dès qu'ils sont parcourus par un courant électrique (noté I en ampère), va créer un champ magnétique. Le flux magnétique qui en résultara est noté Φ (se prononce phi) et s’exprime en Weber (Wb).
On exprime également Les dipôles self ou bobine seront également dimensionnés en utilisant le valeur inductance qui sera alors une grandeur physique dont l'unité est le Henry (H).
Le flux magnétique Φ est proportionnel à l'inductance et l'intensité du courant qui la traverse.

On rencontre une inductance dans les bobinages d'un transformateur, ces bobines permettent en effet d'élever ou d'abaisser la tension et à l'inverse pour le courant. Des bobines sont également présentes dans le contacteur ou le télérupteur ou un contacteur, elle permet l'apparition d'un champ magnétique permettant le déplacement déplacer du contact électrique nécessaire à la circulation du courant (fermeture du ou des contacts). Les bobinages se retrouvent également dans les moteurs électriques, il permettent la création du champ magnétique qui permet de les faire tourner.

2. Mesures expérimentales :

A l'aide d’un oscilloscope, on mesure sur la voie 1 le courant (rouge) et sur la voie 2 la tension (vert) de la bobine du contacteur.

Cette bobine est une inductance, elle se note L et son unité est le Henry (H).

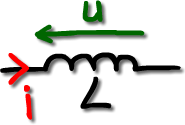
Dessiner le raccordement de l'oscilloscope pour visualiser les signaux sur l'oscilloscope :

Calibre de la voie 1	Calibre de la voie 2	Base de temps
0,5A/DIV	11V/DIV	2ms/DIV

3. Détermination des caractéristiques de la tension et du courant :

Pour déterminer les caractéristiques du courant et de la tension il va falloir interpréter les informations données par les sinusoïdes.

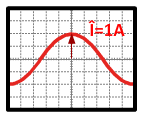
Le courant maximal : il est noté Î ou Imax Pour déterminer Î il faut compter le nombre de carreaux ou division (DIV) de l'axe des abscisses à la partie maximale de la sinusoïde de i(t) Il y a 2 carreaux soit 2 divisions. Le calibre de la voie 1 l'oscilloscope est 0,5A/DIV alors : Î = DIV × Calibre     Î = DIV × Calibre = 2 × 0,5 = 1 A

Le courant efficace : il est noté I

I = Î / √2

    I = Î / √2 = 2 / √2 = 1,41 A

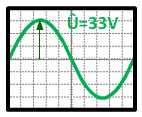
La tension maximale : elle est notée Û ou Umax    U = DIV × Calibre     U = DIV × Calibre = 3 × 11 = 33 V

La tension efficace : elle est notée U

U = Û / √2

    U = Û / √2 = 33 / √2 = 23,3 V

Un signal est dit périodique si les variations de son amplitude se reproduisent au bout d'un certain temps appelé période et notée T (en secondes ou millisecondes). Pour déterminer la période, il faut utiliser la base de temps et compter le nombre de divisions correspondant à une période du signal :     T = DIV × Base de Temps = 10 × 2ms = 20 ms.

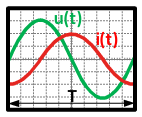La fréquence d'un signal périodique correspond au nombre de périodes par seconde, elle est notée F et s'exprime en Hert (Hz)

Pour déterminer la fréquence il faut connaître la période est utiliser la formule :

F = 1 / T

    F = 1 / 20 ms = 1 / 0,02 = 50 Hz

La pulsation est image de la fréquence, elle est notée ω et s'exprime en rad/s.

Pour déterminer la pulsation il faut connaître la fréquence est utiliser la formule :

ω = 2.π.F

    ω = 2.π × 50 = 100π rad/s = 314,16 rad/s

On peut voir que les 2 signaux (tension et courant) sont décalés l'un par rapport à l'autre.

Le courant et la tension sont dit en quadratures c'est à dire qu'il y a un déphasage de 90° entre la tension et le courant.

Si le tension est prise pour origine, le déphasage du courant par rapport à la tension est φ = 90° = π/2 rad

Le courant et la tension sont déphasés car le récepteur est inductif (bobine).

La tension est en avance de 90° ou π/2 rad par rapport au courant.

La tension est en quadrature avant par rapport au courant.

4. Allures de la tension et du courant et vecteur de Fresnel :

Sur l'animation ci-dessous et mettre le vecteur de la tension U sur l'origine et le vecteur du courant I en retard de 90°C.

On se rend compte que la tension u(t) est en quadrature avance (90°) sur le courant i(t) :

Lorsqu'un courant i(t) parcours une impédance purement inductive celui-ci est en retard de 90° par rapport à la tension u(t).

5. Équation du courant et de la tension :

Un signal sinusoïdal (tension ou courant) est une fonction du temps : u(t) ou i(t)

Les équations qui permettent d’obtenir à chaque instant la valeur de u ou de i sont de la forme :

La Tension est prise pour origine φ = 0 :

u(t)= Û × sin (ωt)

    u : valeur instantanée de la tension en Volt (V)

    Û : tension maximale en Volt (V)

    ω : pulsation (rad/s)

    t : temps en seconde (s)

Pour une impédance purement inductive le Courant est en retard de 90° ou π/2 donc φ = -π/2 :

i(t)= Î × sin (ωt - π/2)

    i : valeur instantanée du courant en Ampère (A)

    Î : intensité maximale en Ampère (A)

    ω : pulsation (rad/s)

    t : temps en seconde (s)

    φ = -π/2 : angle de déphasage par rapport à l'origine (tension) (rad)

Les 2 équations des signaux mesurés au début du cours ont pour équations :

u(t)= Û × sin (ωt) = u(t) = 24√2 sin (100πt)

i(t)= Î × sin (ωt) = u(t) = 4√2 sin (100πt - π/2)

6. L'inductance sous tension sinusoïdale monophasée (Réactance) :

Une inductance se note L et s'exprime en Henry (H).

Une impédance dans un montage électrique n'est jamais purement inductive.

L'impédance d'une inductance réelle (non parfaite) contient une part de résistance et se note donc :

Z = R + j.XL

    Z : impédance réelle en Ω

    R : résistance en Ω

    X_L : réactance purement inductive en Ω

La réactance d'un circuit électrique j.X_L correspond à la partie imaginaire de l'impédance induite par la présence de l'inductance (L) dans le circuit.

Si une bobine est parcourue par un courant alors elle génère un champ magnétique.

L'inductance (bobine) a pour effet de lisser les variations du courant.

XL = 2.π.f.L = L.ω

    X_L : réactance purement inductive en Ω

    f : fréquence en Hz

    L : inductance en H

    ω : pulsation en rad/s

Dans un circuit à courant continu la réactance est nulle X_L = 0Ω.

Pour une impédance purement inductive on peut noter l'impédance Z_L :

ZL = XL = L.ω

    Z : impédance purement inductive en Ω

    R : résistance en Ω

    X_L : réactance purement inductive en Ω

    L : inductance en H

    ω : pulsation en rad/s

Lorsqu'une impédance purement inductive est parcourue par un courant alternatif sinusoïdal la formule ci-dessous s'applique :

U = ZL × I = L.ω × I

    U : Tension efficace en Volt (V)

    I : Courant efficace en Ampère (A)

    Z : Impédance du circuit en Ohms (Ω)

    L : inductance en H

    ω : pulsation en rad/s

La tension u(t) d'une impédance purement inductive est en quadrature avance sur le courant i(t) :

φ = 90° = π/2 rad

7. Conclusion :

Lorsqu'une impédance purement inductive est parcourue par un courant alternatif sinusoïdal sous tension monophasée :

8. Exercices :

Le QCM présent sur ce lien permet de vérifier ses connaissances sur le cours inductance en alternatif sinusoïdal monophasé.