> >

Le condensateur en alternatif sinusoïdal monophasé

Découverte du condensateur électrique dans un montage alternatif sinusoïdal monophasé

Le condensateur ou capacité est un composant électrique présent dans de nombreux appareils en électrotechnique. Comprendre comment le condensateur affecte le courant et la tension dans un circuit électrique est fondamental pour tout électricien travaillant dans le domaine. Sur cette page, vous trouverez des explications pour visualiser les signaux de courant et de tension sur un circuit capacitif en alternatif monophasé et comment analyser l'influence du condensateur sur ces signaux.

Sommaire :
• 1. Mesures expérimentales
• 2. Détermination des caractéristiques de la tension et du courant
• 3. Allures de la tension et du courant et vecteur de Fresnel
• 4. Équation du courant et de la tension
• 5. Le condensateur sous tension sinusoïdale monophasée
• 6. Groupement de condensateur
• 7. Conclusion
• 8. Exercices

1. Mesures expérimentales :

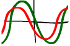
A l'aide d’un oscilloscope, on mesure sur la voie 1 le courant (rouge) et sur la voie 2 la tension (vert) du condensateur.

Ce condensateur se note C et son unité est le Farad (F).

Le Farad est une grandeur très grande de ce fait on utilise souvent les sous-multiples :

1 Farad	1 F
1 milliFarad	10^-3 F = 1 mF
1 microFarad	10^-6 F = 1 µF
1 nanoFarad	10^-9 F = 1 nF
1 picoFarad	10^-12 F = 1 pF

Un condensateur ne laisse pas passer le courant continu (il le bloque) par contre il laisse passer le courant alternatif.

Un condensateur est constitué de deux conducteurs séparés par un isolant (voir le symbole).

Représentation d'un condensateur (capacité)

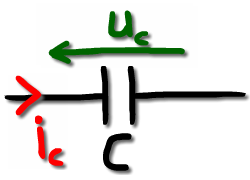
Le condensateur est égal au rapport entre la quantité d'électricité Q (en Coulombs) qu'il peut emmagasiner et de la tension U (en Volts) à ses bornes :

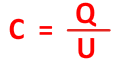
Dessiner le raccordement de l'oscilloscope pour visualiser les signaux sur l'oscilloscope :

Mesure expérimentale à l'aide d'un oscilloscope du courant et de la tension sur un condensateur (purement capacitif)

Calibre de la voie 1	Calibre de la voie 2	Base de temps
1A/DIV	80V/DIV	2ms/DIV

La mesure ci-dessus permet de visualiser les signaux courant et tension du condensateur présents sur un volet roulant tubulaire.

2. Détermination des caractéristiques de la tension et du courant :

Pour déterminer les caractéristiques du courant et de la tension il va falloir interpréter les informations données par les sinusoïdes.

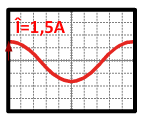
Le courant maximal se note Î ou I_max

Pour déterminer Î il faut compter le nombre de carreaux ou division (DIV) de l'axe des abscisses à la partie maximale de la sinusoïde de i(t)

Il y a 1,5 carreaux soit 1,5 divisions. Le calibre de la voie 1 l'oscilloscope est 1A/DIV alors :

Î = DIV × Calibre

Î = DIV × Calibre = 1,5 × 1 = 1,5 A

Le courant efficace se note I

I = Î / √2

I = Î / √2 = 1,5 / √2 = 1,06 A

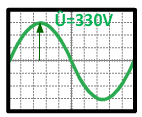
La tension maximale se note Û ou U_max

U = DIV × Calibre

U = DIV × Calibre = 3 × 110 = 330 V

La tension efficace se note U

U = Û / √2

U = Û / √2 = 330 / √2 = 233,34 V

Un signal est dit périodique si les variations de son amplitude se reproduisent au bout d'un certain temps appelé période et notée T (en secondes ou millisecondes). Pour déterminer la période, il faut utiliser la base de temps et compter le nombre de divisions correspondant à une période du signal : T = DIV × Base de Temps = 10 × 2ms = 20 ms.

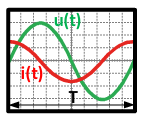
Un signal est dit périodique si les variations de son amplitude se reproduisent au bout d'un certain temps appelé période et notée T (en secondes ou millisecondes).

Pour déterminer la période, il faut utiliser la base de temps et compter le nombre de divisions correspondant à une période du signal :

T = DIV × Base de Temps = 10 × 2ms = 20 ms.

La fréquence d'un signal périodique correspond au nombre de périodes par seconde, elle est notée F et s'exprime en Hert (Hz)

Pour déterminer la fréquence il faut connaître la période est utiliser la formule :

F = 1 / T

F = 1 / 20 ms = 1 / 0,02 = 50 Hz

La pulsation est image de la fréquence, elle est notée ω et s'exprime en rad/s.

Pour déterminer la pulsation il faut connaître la fréquence est utiliser la formule :

ω = 2.π.F

ω = 2.π × 50 = 100π rad/s = 314,16 rad/s

On peut voir que les 2 signaux (tension et courant) sont décalés l'un par rapport à l'autre.

Le courant et la tension sont dit en quadratures c'est à dire qu'il y a un déphasage de 90° entre la tension et le courant.

Si le tension est prise pour origine, le déphasage du courant par rapport à la tension est φ = -90° = -π/2 rad

Le courant et la tension sont déphasés car le récepteur est capacitif (condensateur).

Le courant est en avance de 90° ou π/2 rad par rapport à la tension.

3. Allures de la tension et du courant et vecteur de Fresnel :

Sur l'animation ci-dessous et mettre le vecteur de la tension U sur l'origine et le vecteur du courant I en avance de 90°C.

Animation interactive du cercle trigonométrique

On se rend compte que le courant i(t) est en quadrature avance (90°) sur la tension u(t) :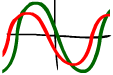

Lorsqu'un courant i(t) parcours une impédance purement capacitive (réactance) celui-ci est en avance de 90° par rapport à la tension u(t).

4. Équation du courant et de la tension :

Un signal sinusoïdal (tension ou courant) est une fonction du temps : u(t) ou i(t)

Les équations qui permettent d’obtenir à chaque instant la valeur de u ou de i sont de la forme :

La Tension est prise pour origine φ = 0 :

u(t)= Û × sin (ωt)

u : valeur instantanée de la tension en Volt (V)

Û : tension maximale en Volt (V)

ω : pulsation (rad/s)

t : temps en seconde (s)

Pour une impédance purement capacitive le courant est en avance de 90° ou π/2 :

i(t)= Î × sin (ωt + π/2)

i : valeur instantanée du courant en Ampère (A)

Î : intensité maximale en Ampère (A)

ω : pulsation (rad/s)

t : temps en seconde (s)

π/2 : angle de déphasage par rapport à l'origine (tension) (rad)

Les 2 équations des signaux mesurés au début du cours ont pour équations :

u(t)= Û × sin (ωt) = u(t) = 330 sin (100πt)

i(t)= Î × sin (ωt) = u(t) = 1,5 sin (100πt + π/2)

5. Le condensateur sous tension sinusoïdale monophasée (Réactance) :

Une Condensateur se note C et s'exprime en Farad (F).

Le condensateur stocke momentanément de l'énergie puis la restitue (réservoir d'énergie).

Cette propriété est utilisée dans les convertisseurs AC/DC des appareils électroniques (courant continu) pour "lisser" la tension produite par l'alimentation.

Le condensateur a pour effet de lisser les variations de la tension.

Une impédance dans un montage électrique n'est jamais purement capacitive.

L'impédance d'un Condensateur réel (non parfait) contient une part de résistance et se note donc :

Z = R - j.X_C

Z : impédance réelle en Ω

R : résistance en Ω

X_C : réactance purement capacitive en Ω

La réactance d'un circuit électrique j.X_C correspond à la partie imaginaire de l'impédance induite par la présence du condensateur (C) dans le circuit.

Pour connaître le module de l'impédance |Z| il faut faire :

$\|Z\| = \sqrt {R^2 + X^2}$

Pour un élément purement capacitif, l'impédance est égale à la valeur absolue de la réactance :		Z = \|X\|

X_C : réactance purement capacitive en Ω

f : fréquence en Hz

C : Condensateur en F

ω : pulsation en rad/s

Dans un circuit à courant continu la réactance est nulle X_C = 0Ω.

Pour une impédance purement capacitive on peut noter l'impédance Z_C :

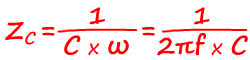
Z : impédance purement capacitive en Ω

R : résistance en Ω

C : Condensateur en F

ω : pulsation en rad/s

Lorsqu'une impédance purement capacitive est parcourue par un courant alternatif sinusoïdal la formule ci-dessous s'applique :

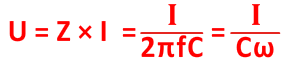
U : Tension efficace en Volt (V)

I : Courant efficace en Ampère (A)

Z : Impédance du circuit en Ohms (Ω)

C : Condensateur en F

ω : pulsation en rad/s

La tension u(t) d'une impédance purement capacitive est en quadrature retard sur le courant i(t) :

φ = -90° = -π/2 rad

6. Groupement de condensateur :

La détermination du groupement de condensateurs se fait à l'inverse de celui des résistances.

7. Conclusion :

Lorsqu'une impédance purement capacitive est parcourue par un courant alternatif sinusoïdal sous tension monophasée :

Formule des puissances pour un dipôle purement capacitif

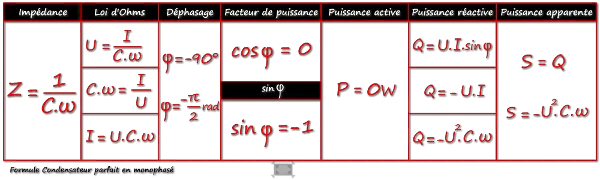
8. Exercices :

Le QCM présent sur ce lien permet de vérifier ses connaissances sur le cours condensateur en alternatif sinusoïdal monophasé.